MATH6100 Calculus 1
|
The slope of a horizontal line is |
0 |
|
Sketch the lines
X=1, x=2, and x=3 tangent to the curve given in figure 7. Estimate the slope
of each of the tangent lines you drew. |
(2 answers) The slope of the tangent line x=2
is 0. The slope of the tangent lines at
x=1 is 1 and at x=3 is -1. |
|
The slope of the
tangent line is called the |
Derivative |
|
The 2 divisions of
Calculus are: |
Integral Differential |
|
The process of
taking the limit of a sum of little quantities is called |
Integration |
|
The following
problems could be solved by differential calculus: |
largest or smallest volume of a
solid rate or speed |
|
Calculus was
developed by Leibniz and |
Newton |
|
If a tangent line
is inclined 45 degrees, then what is the slope the tangent line? |
1 |
|
Find the equation
of a circle with radius=6 and center C(2,-5). (write the required exponent
after the ^ symbol; write the numerical coefficient of each term to complete
the required equation) |
X ^ 2 + y
^ 2 – 4 x + 10 y
– 7 = 0 |
|
Find the slope and
midpoint of the line segment from P(2,-3) to Q(2+n,-3+5n). |
Slope = 5 midpoint (0.5n+ 2 , 2.5 n-3) |
|
Find an equation
describing all points P(x,y) equidistant from Q(-3,4) and R(1,-3). (use the
general equation of a line |
8 x
– 14 y + 15 = 0 |
|
Find the line which
goes through the point (2,-5) and is perpendicular to the line 3y-7x=2.
(write the numerical coefficient of each term to complete the required
equation) |
3 x + 7 y + 29 =
0 |
|
Find the slope of
the line which is tangent to the circle with center C(3,1) at the point
P(8,13). |
Slope of the tangent line
= -5 / 12 |
|
Find the slope of
the line passing through the points (3,-4) and (-6,9). Use decimal value for
your final answer. |
-1.44 |
|
Find the length and
midpoint of the interval from x=9 to x=-2. (use decimal values for fractional
answer) |
Length = 11 and
midpoint = 3.5 |
|
Find the equation
of the line which goes through the point (3,10) and is parallel to the line
7x-y=1. |
7 x
– y – 11 = 0 |
|
Find the equation
of the line passing through (-2,3) and perpendicular to the line 4x=9-2y. Use
the general equation of the line for your final answer. |
X – 2 y
+ 8 = 0 |
|
The figure shows
the distance of a car from a measuring position located on the edge of a
straight road. (a) What was the
average velocity of the car from t=10 to t=30 seconds? |
a) average velocity = 10 feet/second |
|
(b) What was the
average velocity of the car from t=20 to t=25 seconds? |
(b) average velocity = -20 feet/second |
|
The figure shows
the temperature during a day in a place. How fast is the temperature changing
from 1:00 P.M. to 7:00 P.M.? Round-off your answer to 2 decimal places. |
-1.67 0F/hour |
|
From the figure
shown, A(x) is defined to be the area bounded by the x and y axes, the
horizontal line y=3 and the vertical line at x. For example A(4)=12 is the
area of the 4 by 3 rectangle (a) Evaluate A(2.5) |
7.5 square units |
|
(b) Evaluate A(4) -
A(1) |
9 square units |
|
For f(x) = 3x-2 and
g(x) = x2+1, find the composite function defined by f o g(x) and g o f(x). |
f o g(x) = 3x^2+1 g o f(x) = 9x^2-12x+5 |
|
Refer to the
figure. Which of the following represents the graph drawn in red? Select one: |
g(x)-1 |
|
An enrollment slip
indicates a specific down payment based from the number of units enrolled by
a student as follows: for number of units from 1 to 9, down payment is Php
5000; for number of units from 10 to 15, down payment is Php 10,000; and a
down payment of Php 15,000 for units from 16 to 21. Which of the
multiline functions define E(d), the down payment due on specific number of
units enrolled. Unit is of integer type |
|
|
Evaluate f(3),
g(-1), and h(4) |
f(3) = 1 g(-1) = -2 h(4) = 1 |
|
After evaluating
g(-4), g(-1) and g(3), choose which graph represents the given conditions. |
|
|
A state has just
adopted the following state income tax system: no tax on the first $10,000
earned, 1% of the next $10,000 earned, 2% of the next $20,000 earned, and 3%
of all additional earnings. Write a multiline function for T(x), the state
income tax due on earnings of x dollars. |
|
|
Given g(x) =
(x+3)/(x-1). Evaluate g(5) and g(2n+1). |
g(5) = 2 g(2n+1) = 1+(2/n) |
|
A function f is
given by f(7-11x) = 3x3 - 10x. Evaluate f(-4). |
f(-4) = -7 |
|
A __ assigns a
unique output element in the range to each input element from the domain. |
function |
|
For y=f(x), |
x is the domain, and y is the
range |
|
Given f(x) = x3 -
4x2 +2, f(2) when evaluated is |
-6 |
|
Which of the
following figures represents the graph of a function? |
Figure 2 |
|
Let f(x) = 3x+2 and
g(x) = 2x+A. Find a value for A so that f(g(x)) = g(f(x)). |
f(g(x)) = 6x+3A+2 g(f(x)) = 6x+A+4 A = 1 |
|
For f(x) = |9-x|
and g(x) = sqrt(x-1). Evaluate fog(1). |
f(g(1) = 9 |
|
Given the function
f(x)=3x-4, evaluate: (a) f(x-2), (b) f(x)-f(2), (c) f(1)/f(3), and (d)
f(1/3). Use fraction as final answer, if any. |
(a) 3x-10 (b) 3x-6 (c) -1/5 (d) -3 |
|
Find the slope of
the line through (0,0) and (x-1, x2 -1). |
m = x+1 |
|
From the figure
shown, find the values of f(2), f(-1) and f(0). |
f(2) = 5 f(-1) = 2 f(0) = 1 |
|
From the graph
shown, find the values of f(-3), f(-1), f(0), and f(1). |
f(-3) = -1 f(-1) = 1 f(0) = 0 f(1) = 1 |
|
Let f(x) = -x 4
-x-1, evaluate f(-1) and -2f(1). |
f(-1) = -1 -2f(1) = 6 |
|
What values of x
will make the statement x+5=3 or x2=9. |
x = -2 or (x = 3 and x = -3 ) |
|
What is the slope
of the line through (3,9) and (x,y) for y=x2 and x=2.97? x=3.001? x=3+h? What
happens to this last slope when h is very small (close to 0)? Round-off your
answers to 2 decimal places, whenever possible. |
Slope at x=2.97 = 5.97 Slope at x=3.001 = 6.00 Slope at x=3+h = 6+h Slope when h is close to 0 = 6 |
|
What is the slope
of the line through (2,4) and (x,y) for y = x2+ x - 2 and x=1.99? x=2.004?
x=2+h. What happens to this last slope when h is very small? |
when x=1.99: m = 4.99 when x=2.004: m = 5.00 when x=2+h:m = 5+h when h approaches 0: m = 5 |
|
What is the slope
of the line through (-1,-2) and (x,y) for y = x2+ 2x + 1 and x=-0.90?
x=-1.05? x=h1? What happens to this last slope when h is very small?
Round-off your answers to 2 decimal places whenever possible. Use the ^
symbol to express the exponent of a variable, i.e. x^2 (x squared) |
when x=-0.90: m = 2 when x=-1.05: m = 3.3 when x=h-1: m = h^2+1 /h when h approaches 0: m = 1 |
|
The figure shows
the distance of a car from a measuring position located on the edge of a
straight road. (a) What was the
average velocity of the car from t=0 to t= 20 sec? (b) What was the
average velocity from t=10 to t=30 sec? (c) About how fast
was the car traveling at t=15 sec? |
(a) V = 15 ft/sec (b) V = -5 ft/sec (c) V = 20 ft/sec |
|
Define A(x) to be
the area bounded by x and y axes, the line y=x+1, and the vertical line at x. (a) Evaluate A(2)
and A(3) (b) What area would
A(3) - A(1) represent? |
(a) A(2) = 4 square units A(3) = 7.5 square units (b) A(3) - A(1) = 6 square units |
|
The graph shows the
population growth of bacteria on a petri plate. If at t=10 days, the
population grows to 4600 bacteria, find the rate of population growth from
t=9 to t= 10 days? |
rate of growth = 400 |
|
Write the
contrapositive of the statement: If x2 + x - 6 = 0 then x=2 or x=-3. |
Answer: If x = - 2 and x = 3 then
x2 + x - 6 is not equal to 0 |
|
The slope of the
line through (5,15) and (x+8, x2 -2x) is |
x-5 |
|
Given g(t) =
t+5t−1t+5t−1, evaluate: (a) g(5) and (b) g(2s - 5) |
(a) g(5) = 5/2 (b) g(2s-5) = s/s-3 |
|
Let f(x) = -x 4
-x-1, evaluate f(-1) and -2f(1). |
f(-1) = -1 -2f(1) = 6 |
|
Let f(x)=-1-x-2x2 ,
evaluate f(x+h)−f(x)hf(x+h)−f(x)h Factor out the negative sign for the final
answer, if any |
-(4x+2h+1) |
|
Which of the
following are negation of the statement: f(x) and g(x) are polynomials. |
f(x) or g(x) is a polynomial f(x) and g(x) are not polynomials |
|
Find the slope of
the line through (-5,3) and (x+1, x-2). |
x-5/x+6 |
|
Write the
contrapositive of the statement: If x>3, then x2>9. Use words or phrase
for your answer. |
If x2 <= 9, then x <= 3 |
|
Let f(x) = 2-x 2 ,
evaluate (a) f(x+1) and (b) f(x)+f(1) |
(a) f(x=1) = -x 2 - 2x+1 (b) f(x) + f(1) = -x 2+3 |
|
If a and b are real
numbers, then (a+b)2 = a2+b2 . |
False |
|
Which of the
following is the contrapositive for the statement: If your car is properly
tuned, it will get at least 24 miles per gallon. |
If your car will not get at least
24 miles per gallon, then it is not properly tuned. |
|
If f(x) and g(x)
are linear functions, the f(x) + g(x) is a linear function |
True |
|
Let f(x)=1-(x-3)2 ,
evaluate: (a) f(x+3), (b) f(3-x), and (c) f(2x+1). |
(a) 1 - x 2 (b) 1 - x 2 (c) -4 x 2 + 8x-3 |
|
Which of the
following will make the statement x2+3 > 1 true? |
x is greater than or equal to -1 |
|
Let f(x) = 1-(x-1)2
evaluate (a)f(2)f(3) and (b)f(23)(a)f(2)f(3) and (b)f(23 |
(a) Answer 0 (b) Answer 8/9 |
|
Let f(x) = 2-x 2 ,
evaluate (a) f(x+1) and (b) f(x)+f(1). |
(a) f(x=1) = -x 2 - 2x+1 (b) f(x) + f(1) = -x 2+ 3 |
|
Find the slope of
the line through (-3-1) and (x+3, y+1). |
x-5/x+6 |
|
From the graph
shown, find: a. f(-1) b. f(0) c. 3f(2) d. the value of x
that corresponds to f(x)=0 |
a. f(-1) = 2 b. f(0) = 1 c. 3f(2) = -14 d. x = 0 |
|
Let A =
{1,2,3,4,5}, B = {0,2,4,6}, and C = {-2,-1,0,1,2,3}. Which of the values of x
will satisfy each statement? |
x is in A or x is in C |
|
Find the slope of
the line through (0,0) and (x-1, x2 |
m = x+1 |
|
Which graph
corresponds to f(x) = √x? |
|
|
Which graph
represents the function f(x) = {2 if x ≤
-1} {x2 if x > -1} |
|
|
Evaluate limx→0cos2x−1cosx−1limx→0cos2x−1cosx−1 |
4 |
|
Write the
contrapositive of the statement: I feel good when I jog. Answer: When I
don't jog, I feel |
Bad |
|
Evaluate limx→3x4−812x2−5x−3limx→3x4−812x2−5x−3 |
108 / 7 |
|
Write the negation
of the statement: 8 is a prime number. 8 is |
not a prime number |
|
Evaluate limx→1x13−1x14−1limx→1x13−1x14−1 |
4 / 3 |
|
Evaluate limx→103x−5−−−−−√5limx→103x−55 |
1 |
|
Every vertical line
on the Cartesian plane intersects the x-axis. |
True |
|
Evaluate limx→43−x+5−−−−√x−4limx→43−x+5x−4 |
1 / 5 |
|
Evaluate limx→35x2−8x−13x2−5limx→35x2−8x−13x2−5 |
2 |
|
Which values of x
will make the statement x+5=3 or x2=9 true? |
-2 or (3 and -3) |
|
The sum of two
prime numbers is a prime. |
false |
|
Use the function h
defined by the graph shown to determine the following limits: (a) limx→2h(5−x)limx→2h(5−x) (b) limx→0h(3+x)−h(3) |
(a) 1 (b) -2 |
|
At which values of
x is the function f(x)=x2+x−6x−2f(x)=x2+x−6x−2continuous and discontinuous? |
continuous at x = -3 discontinuous at x = 2 |
|
Use the function h
defined by the graph below to determine the following limits: (a) limx→2x+h(x)limx→2x+h(x) b) limx→3h(x2) |
(a) 3 (b) 3/4 |
|
Use the graph below
to determine the right-hand limit of the function f(x) at: (a) x=-2 (b) x=10 |
(a) undefined (b) 0 |
|
Use the functions f
and g defined by the graphs as shown to determine the following limits: (a) limx→1(f(x)xg(x))limx→1(f(x)xg(x)) (b) limx→1f(g(x)) |
(a) 0 (b) 5/4 |
|
hich values of x is
the function from the graph shown continuous? State the answers from the
least to the highest, if there would be more than one |
x = -1 |
|
Use the function f
defined by the graph shown to determine the following limits: (a) limx→1+f(x)limx→1+f(x) (b) limx→1−f(x) |
(a) 2 (b) -1 |
|
Use the Bisection
Algorithm Method to find the root of the given function to an interval of
length less than or equal to 0.1. Answer should be up to one decimal place
only. f(x) = x2 - 2 on [0,3] |
1 / 4 |
|
(a) limx→2h(2x−2)limx→2h(2x−2) (b) limx→2h(1+x) |
(a) 1 (b) 1 |
|
Use linear equation
to estimate e0.06 . Choose a value of 'a' to produce a small error. |
e 0.06 = 1.06 |
|
Determine all the
critical points for the function. f(x)=xex2 |
does not have any critical points |
|
Determine whether the graph is continuous or not continuous. |
Not Continuous |
|
There are 50 apple
trees in an orchard. Each tree produces 800 apples. For each additional tree
planted in the orchard, the output per tree drops by 10 apples. How many
trees should be added to the existing orchard in order to maximize the total
output of trees? |
x = 15 additional trees P =r 42250 apples |
|
Use chain rule to
calculate dydxdydx of y=sin(4x3+3x+1)y=sin(4x3+3x+1) |
dydx=(12x2+3)cos(4x3+3x+1)dydx=(12x2+3)cos(4x3+3x+1) |
|
Find a value for B
so that the line y = 10x – B, goes through the point (5,-5). |
B = 55 |
|
For all positive
real numbers a and b, if a > b, then a2 > b2 |
TRUE |
|
Determine whether
the graph is continuous or not continuous. |
Continuous |
|
You are standing at
the edge of a slow-moving river which is one mile wide and wish to return to
your campground on the opposite side of the river. You can swim at 2 mph and
walk at 3 mph. You must first swim across the river to any point on the
opposite bank. From there walk to the campground, which is one mile from the
point directly across the river from where you start your swim. What route
will take the least amount of time? |
x ≈ 0.89 mi. Shortest possible time: T ≈ 0.71 hr. |
|
Determine whether
the graph is continuous or not continuous. |
Not Continuous |
|
Find an equation of
the line tangent to the graph of x2+(y−x)3=9x2+(y−x)3=9 at x=1 |
y=76x+136y=76x+136 |
|
Use linear
approximations to estimate 1–√46146. Choose a value of "a" to
produce a small error |
1–√46=f(146)≈L(146)146=f(146)≈L(146)
= 12.08 |
|
Find the dimensions
(radius r and height h) of the cone of maximum volume which can be inscribed
in a sphere of radius 2. |
r ≈ 1.89 h ≈ 2.67 V ≈ 9.93 |
|
Find the slope and
concavity of the graph pf x2y+y4=4+2xx2y+y4=4+2x at the point (-1,1) |
Slope = 4545, Concavity =
downward |
|
A container in the
shape of a right circular cylinder with no top has surface area 3 ft.2 What
height h and base radius r will maximize the volume of the cylinder? |
r = 1 ft. h = 1 ft. V = 3.14 ft3 |
|
If a and b are real
numbers then (a + b)2 = a2 + b2 |
False |
|
Assume that y is a
function of x. Find y1=dydxy1=dydx for
cos2x+cos2y=cos(2x+2y)cos2x+cos2y=cos(2x+2y) |
y1=cosxsinx−sin(2x+2y)sin(2x+2y)−cosysinyy1=cosxsinx−sin(2x+2y)sin(2x+2y)−cosysiny |
|
Find a linear
approximation to h(t)=t4−6t3+3t−7h(t)=t4−6t3+3t−7 at t=−3t=−3. |
L(t) = 227 - 267 (t + 3) = -267 t
- 57 |
|
Find the local
extreme values of the given function: f(x)=x4−6x2f(x)=x4−6x2 |
Local minimum: (-1.73, -9) Local maximum:(1.73, -9) |
|
Use chain rule to
calculate dydxdydx of y = tan (e3x√)(e3x) |
dydx=−sec2(e3x−−√)3e3x√23x−−√dydx=−sec2(e3x)3e3x23x |
|
Use chain rule to
calculate dydxdydx of y=cos4(7x3)y=cos4(7x3) |
dydx=−84x2cos3(7x3)sin(7x3)dydx=−84x2cos3(7x3)sin(7x3) |
|
(\Large \lim_{x
\rightarrow 3} (2x + 1) = 7 \) What values of x guarantee that f(x) = 2x + 1
is within 0.04 units of 7? If x is within _____ units of 3, then f(x)
is within 0.04 units of 7. |
0.02 |
|
Find the point of
intersection and the angle between x - y = 32 and 3x - 8y = 6. |
Point of Intersection = (50 , 18
) Angle of Intersection = -24.44 0
(round-off to 2 decimal places) |
|
If f(x) and g(x)
are linear functions then f(x)g(x) is a linear function. |
False |
|
Use the function h
defined by the graph below to determine the following limits: (a) limx→2(xlimx→2(x . h(x−1))h(x−1)) (b) limx→0h(3+x)−h(3)h(x)limx→0h(3+x)−h(3)h(x) |
(a) 8/3 (b) -6/5 |
|
Determine all the
critical points for the function. f(x)=x2ln(3x)+6f(x)=x2ln(3x)+6 |
0.20 |
|
Write the
contrapositive of the statement: If I exercise and eat right, then I will be
healthy. Don't use contractions in your answer |
If I am not healthy, then I do not exercise and
eat right. |
|
Which of the
following equations is the line perpendicular to 2x – 3y = 9? |
3x + 2y =10 |
|
Determine whether
the graph is continuous or not continuous. |
Continuous |
|
Given a function f,
an interval [a,b] and a value V. Find a value c in the interval so that
f(c)=V. Apply the Intermediate Value Theorem. (a)f(x)=x2f(x)=x2
on [0,3], V = 2 (b)f(x)=sinx on
[0,π2],V=12f(x)=sinx on [0,π2],V=12 |
(a) c = -1.41 ; c = 1.41 (b) c = 0.52 |
|
Evaluate limx→3x4−812x2−5x−3limx→3x4−812x2−5x−3 |
108 / 7 |
|
Find an equation of
the line tangent to the graph of y=x2+sinπ2xy=x2+sinπ2x at x = -1 |
y = -2x - 2 |
|
Use implicit
differentiation to finddydxdydx exy=2yexy=2y |
y1=yexy2−xexyy1=yexy2−xexy |
|
(Note: Answers
should be in decimal form. Up to two decimal places only) |
x = 1.5 Smallest sum: S = 8.5 |
|
Which of the
following equations is the line perpendicular to 4y – 7x = 5? |
4x + 7y – 18 = 0 |
|
1. Write the
equation of the line that represents the linear approximation to the function
below at a given point a. f(x) = ln(1 + x); a
= 0; f(0.9) |
y = L(x) = x |
|
2. Use linear
approximation to estimate the given function value. |
f(0.9) = 0.9 |
|
. Compute the
percent error in your approximation by the formula:
|approx−exact|exact|approx−exact|exact |
Percent error: 40.22 % |
|
The slope of the
line from point U(5,13) and the point V(x+1, x2 -3) is |
x+4 |
|
Use chain rule to
calculate dydxdydx of y=x2sec(5x)y=x2sec(5x) |
dydx=−2xsec(5x)+5x2sec(5x)tan(5x)dydx=−2xsec(5x)+5x2sec(5x)tan(5x) |
|
Let f(x) = (x-1)2
and define S(x) to be the slope of the line through the point (0,0) and
(x,f(x)). Evaluate S(6). |
S(6) = 25/6 |
|
(Note: Answers
should be in decimal form only. Up to two decimal places} |
x ≈ 8.77 ft. y ≈ 16.67 ft. L ≈ 17.64 ft. |
|
Evaluate limx→0(x+1)3−1xlimx→0(x+1)3−1x |
3 |
|
Fill in the missing
the numbers to find the correct answer/s: Find two nonnegative numbers whose
sum is 9 and so that the product of one number and the square of the other
number is a maximum. P = xy2 |
x = 3 y = 6 P = 108 |
|
If f(x) and g(x)
are linear functions, then f(x) + g(x) is a linear function. |
True |
|
Use Newton's Method
to find the root of 2x2+5=ex2x2+5=ex accurate to six decimal places in the
interval [3,4]. |
x ≈ 4.36 |
|
(Note: Answer
should be in decimal form. Up to two decimal places only) |
x ≈ 17.32 ft. θ = 30 degrees |
|
Determine whether
the graph is continuous or not continuous. |
Continuous |
|
limx→13x+2=5limx→13x+2=5 What values
of x guarantee that f(x) = 3x + 2 is within 0.05 unit of 5? |
If x is within 0.02 unit distance
of 1, then f(x) is within 0.05 unit of 5. |
|
Determine all the
critical points for the function y=6x−4cos(3x)y=6x−4cos(3x)
x=???+2πn3,n=0,±1,±2,...x=???+2πn3,n=0,±1,±2,...
x=???+2πn3,n=0,±1,±2,...x=???+2πn3,n=0,±1,±2,... |
1.2217; 1.9199 |
|
Assume that y is a
function of x. Find y1=dydxy1=dydx for x−y3y+x2=x+2x−y3y+x2=x+2 |
y1=1−y−3x2−4x3y2+x+2y1=1−y−3x2−4x3y2+x+2 |
|
Evaluate limx→0(x+5)2−25xlimx→0(x+5)2−25x |
10 |
|
Evaluate limx→35x2−8x−13x2−5limx→35x2−8x−13x2−5 |
2 |
|
Write the equation
of the line that represents the linear approximation to the function below at
the given point a. f(x)=e2;a=0;f(0.05)f(x)=e2;a=0;f(0.05) |
f(a) = 7.39 |
|
Use the linear
approximation to estimate the given function value. |
f(0.05) ≈ L (0.05) = 0.05 |
|
Percent error ≈ |
20 |
|
Given f(x) = 2x + 3
and g(x) = x2 . Evaluate . Sample text answer: 3x^2+6x7. Do not use space
between the number, letter and symbol. |
4x^2+12x+9 |
|
Use Newton's Method
to determine x2x2 for f(x)=xcos(x)−x2f(x)=xcos(x)−x2 if x0=1x0=1 |
x2 = 0.74 |
|
Assume that y is a
function of x. Find y1=dydxy1=dydx for (x−y)2=x+y−1(x−y)2=x+y−1 |
y1=2y−2x+12y−2x−1y1=2y−2x+12y−2x−1 |
|
Use chain rule to
calculate dydxdydx of y=e−x2y=e−x2 |
dydx=−2x−x2dydx=−2x−x2 |
|
Locate the critical
points of the following functions. Then use the second derivative test to
determine whether they correspond to local minima or local maxima or whether
the test is inconclusive. |
Critical points: (2, -1/4) and
(10, -1/20) Local minimum: x = -2 Local maximum: x = 10 |
|
Use Newton's Method
to find the root of x4−5x3+9x+3=0x4−5x3+9x+3=0 accurate to six decimal places
in the interval [4,6]. |
x ≈ 4.53 |
|
Identify the
absolute extrema and relative extrama for the following function.
f(x)=x3f(x)=x3 on [-2,2] |
The function has an absolute
maximum of 8 at x = 2 and absolute minimum of -8 at x = - 2. The function has
no relative extrema. |
|
Use the functions f
and g defined by the graphs as shown to determine the following limits: (a) limx→1f(x)+g(x)limx→1f(x)+g(x) (b) limx→2f(x)g(x)limx→2f(x)g(x) |
(a) 2 (b) 4/3 |
|
Determine whether
the graph is continuous or not continuous. |
Not Continuous |
|
Use implicit
differentiation to find dydxdydx (xy+1)3=x−y2+8(xy+1)3=x−y2+8 |
y1=1−3y(xy+1)23x(xy+1)2+2yy1=1−3y(xy+1)23x(xy+1)2+2y |
|
Evaluate limx→7x−3−−−−√limx→7x−3 |
2 |
|
Build a rectangular
pen with three parallel partitions using 500 feet of fencing. What dimensions
will maximize the total area of the pen? |
x = 50 ft. y = 125 ft. A = 6250 ft2 |
|
For the function f(x)=x(x2+1)2f(x)=x(x2+1)2
on [-2,2] Find the critical points and the absolute extreme values of f on
the given interval. |
x=±13−−√x=±13 as the critical
points absolute maximum value of f:
33√163316 absolute minimum value of
f:33√163316 |
|
Assume that y is a
function of x. Find y1=dydxy1=dydx for y=x2y3+x3y2y=x2y3+x3y2 |
y1=2xy3+3x2y21−3x2y2−2x3yy1=2xy3+3x2y21−3x2y2−2x3y |
|
limx→13x+2=5limx→13x+2=5 What values of x
guarantee that f(x) = 3x + 2 is within 0.05 unit of 5? |
If x is within 0.02 unit distance
of 1, then f(x) is within 0.05 unit of 5 |
|
An open rectangular
box with square base is to be made from 48 ft.2 of material. What dimensions
will result in a box with the largest possible volume? |
x = 4 ft. y = 2 ft. V = 32 ft.3 |
|
Write the negation
for the statement: All quadratic equations have solutions. |
not all quadratic equations all
solutions. |
|
Use the function h
defined by the graph shown to determine the following limits: (a) limx→2h(5−x)limx→2h(5−x) (b) limx→0h(3+x)−h(3)limx→0h(3+x)−h(3 |
(a) 3 (b) 3/4 |
|
Use implicit
differentiation to find dydxdydx, x3=x+yx−yx3=x+yx−y |
y1=3x2(x−y)2+2y2xy1=3x2(x−y)2+2y2x |
|
Find the point of
intersection and the angle between y = 4 - 2x and x - y = -1. |
Point of Intersection = (1 , 2 ) Angle of Intersection = -71.56 0 |
|
Find a linear
approximation of f(x)=3xe2x−10f(x)=3xe2x−10 at x = 5 |
L(x) = 15 + 33 (x - 5) = 33 x + 150 |
|
Determine whether
the graph is continuous or not continuous. |
Continuous |
|
Find the point of
intersection and the angle between 2x - 3y = 3 and 4x - 2y = 10. |
Point of Intersection = (3 , 1 ) Angle of Intersection = 29.740 |
|
Consider a
rectangle of perimeter 12 inches. Form a cylinder by revolving this rectangle
about one of its edges. What dimensions of the rectangle will result in a
cylinder of maximum volume? |
r = 4 ft h = 2 ft V ≈ 100.53 ft3 |
|
Evaluate limx→43−x+5−−−−√x−4limx→43−x+5x−4 |
- 1 / 6 |
|
Use chain rule to
calculate dydxdydx of y=(5x2+11x)20y=(5x2+11x)20 |
dydx=(20)(5x2+11x)19(10x+11)dydx=(20)(5x2+11x)19(10x+11) |
|
Determine whether
the graph is continuous or not continuous. |
Not Continuous |
|
Evaluate limx→103x−5−−−−−√5limx→103x−55 |
1 |
|
Which of the
following are integer values of x that will make the statement x>4 and x |
5,6,7,8 |
|
Determine whether
the graph is continuous or not continuous. |
Not Continuous |
|
If x divides 49,
then x divides 30. |
False |
|
Every straight line
on the Cartesian plane intersects the x-axis. |
True |
|
Assume that y is a
function of x. Find y1=dydxy1=dydx for y=sin(3x+4y)y=sin(3x+4y) |
y1=3cos(3x+4y)1−4cos(3x+4y)y1=3cos(3x+4y)1−4cos(3x+4y) |
|
Do the following. Determine the answers by typing the missing numbers
on the spaces provided. Up to two decimal places only: |
|
|
f(x)
= 12 - x 2 ; a = 2 ; f(2.1) |
L(x) = -4 x + 16 |
|
Use linear
approximation to estimate the given function value |
f(2.1) = 7.6 |
|
Compute the percent
error in your approximation by the formula: |approx−exact|exact|approx−exact|exact |
Percent error is: 0.13 % |
|
(Note: Answers
should be in decimal form. Up to two decimal places only) |
Largest possible slope: x = 1 y = 1.5 S = -0.75 Smallest possible slope: x = -1 y = -1.5 S = 0.75 |
|
Find an equation of
the line tangent to the graph of (x2+y2)3=8x2y2(x2+y2)3=8x2y2 at the point
(-1,1) |
y - 1 = x + 2 |
|
A sheet of
cardboard 3 ft. by 4 ft. will be made into a box by cutting equal-sized
squares from each corner and folding up the four edges. Given that variable x
shall be the length of one edge of the square cu from each corner of the
sheet of cardboard, what will be the dimensions of the box with largest
volume? |
x ≈ 0.57 ft, so Length = 2.86 ft Width = 1.86 ft Height = 0.57 ft V ≈ 3.03 ft |
|
Given f(x) = 2x +
3. Evaluate (f°f)(x). Sample text answer: 3x^2+6x-7. Do not use space between
the number, letter and symbol. |
4x+9 |

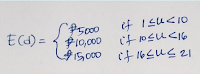















TYVM!luv u!hehe
ReplyDeleteThe slope of a vertical line is: undefined
ReplyDelete